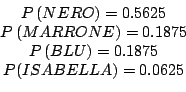Esempi di calcolo delle probabilità

Notazione

Ad ogni genotipo in figura 1 si associa il numero di riga/colonna della matrice in cui compare (e.g. BBDD $\leftrightarrow$1, bbdd $\leftrightarrow$9).

Genitore $\alpha =BbDd$, genitore $\beta =BbDd$ (casella $\left (5,5\right )$ in figura 1)

Le leggi della genetica ci dicono che l'evento certo è dato da:

$$\begin{array}{cccc} I=\left\{ B_{\alpha }B_{\beta }D_{\alph... ....b_{\alpha }b_{\beta }d_{\alpha }d_{\beta }\right\} \end{array}$$

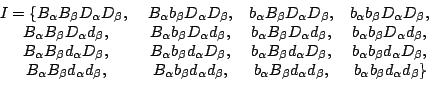
e che ogni evento elementare è equiprobabile, per cui

$$\forall \zeta \in I\quad P\left(\left\{ \zeta \right\} \right)=\frac{1}{\char93 I}=\frac{1}{16}$$

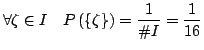
Posto:

$$\begin{array}{c} I_{BBDD}=\left\{ B_{\alpha }B_{\beta }D_{\... ... b_{\alpha }b_{\beta }d_{\alpha }d_{\beta }\right\} \end{array}$$

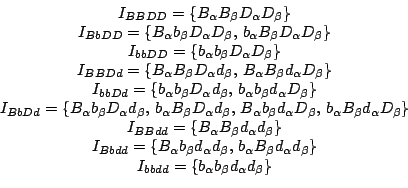
discende immediatamente che:

$$\begin{array}{c} P\left(I_{BBDD}\right)=0.0625\\ P\left(I... ...Bbdd}\right)=0.125\\ P\left(I_{bbdd}\right)=0.0625\end{array}$$

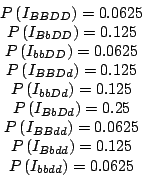
Infine, ponendo

$$\begin{array}{c} NERO=I_{BBDD}\cup I_{BbDD}\cup I_{BBDd}\cu... ...\\ BLU=I_{BBdd}\cup I_{Bbdd}\\ ISABELLA=I_{bbdd}\end{array}$$

si ottiene:

$$\begin{array}{c} P\left(NERO\right)=0.5625\\ P\left(MARRO... ...\\ P\left(BLU\right)=0.1875\\ P(ISABELLA)=0.0625\end{array}$$